In this section, we will begin an examination of the fundamental trigonometric identities, including how we can verify them and how we can use them to simplify trigonometric expressions.
1) We know \(g(x)=\cos x\) is an even function, and \(f(x)=\sin x\) and \(h(x)=\tan x\)are odd functions. What about \(G(x)=\cos ^2 x\), \(F(x)=\sin ^2 x\) and \(H(x)=\tan ^2 x\)? Are they even, odd, or neither? Why? Answer All three functions, \(F,G,\) and \(H\) , are even. This is because \(F(-x)=\sin(-x)\sin(-x)=(-\sin x)(-\sin x)=\sin^2 x=F(x),G(-x)=\cos(-x)\cos(-x)=\cos x\cos x= cos^2 x=H(-x)=\tan(-x)\tan(-x)=(-\tan x)(-\tan x)=\tan2x=H(x)\) 2) Examine the graph of \(f(x)=\sec x\) on the interval \([-\pi ,\pi ]\) . How can we tell whether the function is even or odd by only observing the graph of \(f(x)=\sec x\)? 3) After examining the reciprocal identity for \(\sec t\) , explain why the function is undefined at certain points. Answer When \(\cos t = 0\) , then \(\sec t = 10\) , which is undefined. 4) All of the Pythagorean identities are related. Describe how to manipulate the equations to get from \(\sin^2t+\cos^2t=1\) to the other forms.
For the exercises 5-15, use the fundamental identities to fully simplify the expression. 5) \(\sin x \cos x \sec x\) Answer \(\sin x\) 6) \(\sin(-x)\cos(-x)\csc(-x)\) 7) \(\tan x\sin x+\sec x\cos^2x\) Answer \(\sec x\) 8) \(\csc x+\cos x\cot(-x)\) 9) \(\dfrac\) Answer \(\csc x\) 10) \(3\sin^3 t\csc t+\cos^2 t+2\cos(-t)\cos t\) 11) \(-\tan(-x)\cot(-x)\) Answer \(-1\) 12) \(\dfrac\) 13) \(\dfrac+\sin ^2\theta +\dfrac\) Answer \(\sec^2 x\) 14) \(\left (\dfrac+\dfrac \right )\left (\dfrac \right )-\dfrac\) 15) \(\dfrac+2\sin ^2 x\) Answer \(\sin^2 x+1\) For the exercises 16-28, simplify the first trigonometric expression by writing the simplified form in terms of the second expression. 16) \(\dfrac; \cos x\) 17) \(\dfrac; \sin x\) Answer \(\dfrac\) 18) \(\dfrac+\tan x; \cos x\) 19) \(\dfrac-\cot x; \cot x\) Answer \(\dfrac\) 20) \(\dfrac-\dfrac; \csc x\) 21) \((\sec x+\csc x)(\sin x+\cos x)-2-\cot x; \tan x\) Answer \(\tan x\) 22) \(\dfrac; \sec x\) and \(\tan x\) 23) \(\dfrac-\dfrac; \sec x\) and \(\tan x\) Answer \(-4\sec x \tan x\) 24) \(\tan x; \sec x\) 25) \(\sec x; \cot x\) Answer \(\pm \sqrt<\dfrac+1>\) 26) \(\sec x; \sin x\) 27) \(\cot x; \sin x\) Answer \(\dfrac<\pm \sqrt<1-\sin ^2 x>>\) 28) \(\cot x; \csc x\) For the exercises 29-33, verify the identity. 29) \(\cos x-\cos^3x=\cos x \sin^2 x\) Answer Answers will vary. Sample proof: \(\begin \cos x-\cos^3x &= \cos x (1-\cos^2 x)\\ &= \cos x\sin ^x \end\) 30) \(\cos x(\tan x-\sec(-x))=\sin x-1\) 31) \(\dfrac=\dfrac+\dfrac=1+2\tan ^2x\) Answer Answers will vary. Sample proof: \(\begin \dfrac &= \dfrac+\dfrac\\ &= \sec ^2x+\tan ^2x\\ &= \tan ^2x+1+\tan ^2x\\ &= 1+2\tan ^2x \end\) 32) \((\sin x+\cos x)^2=1+2 \sin x\cos x\) 33) \(\cos^2x-\tan^2x=2-\sin^2x-\sec^2x\) Answer Answers will vary. Sample proof: \(\begin \cos^2x-\tan^2x &= 1-\sin^2x-\left (\sec^2x -1 \right )\\ &= 1-\sin^2x-\sec^2x +1\\ &= 2-\sin^2x-\sec^2x \end\)
For the exercises 34-39, prove or disprove the identity. 34) \(\dfrac-\dfrac=-2\cot x\csc x\) 35) \(\csc^2x(1+\sin^2x)=\cot^2x\) Answer False 36) \(\left (\dfrac \right )\left (\dfrac \right )-2\sin ^2 x=\cos (2x) \) 37) \(\dfrac\sin (-x)=\cos ^2x\) Answer False 38) \(\dfrac=-\sin (-x)\) 39) \(\dfrac=\dfrac\) Answer Proved with negative and Pythagorean identities For the exercises 40-, determine whether the identity is true or false. If false, find an appropriate equivalent expression. 40) \(\dfrac=\sin ^2 \theta\) 41) \(3\sin^2\theta + 4\cos^2\theta =3+\cos^2\theta\) Answer True \(\begin 3\sin^2\theta + 4\cos^2\theta &= 3\sin ^2\theta +3\cos ^2\theta +\cos^2\theta \\ &= 3\left ( \sin ^2\theta +\cos ^2\theta \right )+\cos^2\theta \\ &= 3+\cos^2\theta \end\) 42) \(\dfrac=\sec ^2 \theta\)
In this section, we will learn techniques that will enable us to solve useful problems. The formulas that follow will simplify many trigonometric expressions and equations. Keep in mind that, throughout this section, the term formula is used synonymously with the word identity.
1) Explain the basis for the cofunction identities and when they apply. Answer The cofunction identities apply to complementary angles. Viewing the two acute angles of a right triangle, if one of those angles measures \(x\) , the second angle measures \(\dfrac<\pi >-x\) . Then \(\sin x=\cos \left (\dfrac<\pi >-x \right )\) . The same holds for the other cofunction identities. The key is that the angles are complementary. 2) Is there only one way to evaluate \(\cos \left (\dfrac<5\pi > \right )\) ? Explain how to set up the solution in two different ways, and then compute to make sure they give the same answer. 3) Explain to someone who has forgotten the even-odd properties of sinusoidal functions how the addition and subtraction formulas can determine this characteristic for \(f(x)=\sin (x)\) and \(g(x)=\cos (x)\) . (Hint: \(0-x=-x\)) Answer \(\sin (-x)=-\sin x\), so \(\sin x\) is odd. \(\cos (-x)=\cos (0-x)=\cos x\), so \(\cos x\) is even.
For the exercises 4-9, find the exact value. 4) \(\cos \left (\dfrac<7\pi > \right)\) 5) \(\cos \left (\dfrac<\pi > \right)\) Answer \(\dfrac+\sqrt>\) 6) \(\sin \left (\dfrac<5\pi > \right)\) 7) \(\sin \left (\dfrac<11\pi > \right)\) Answer \(\dfrac<\sqrt-\sqrt>\) 8) \(\tan \left (-\dfrac<\pi > \right)\) 9) \(\tan \left (\dfrac<19\pi > \right)\) Answer \(-2-\sqrt\) For the exercises 10-13, rewrite in terms of \(\sin x\) and \(\cos x\) 10) \(\sin \left (x+\dfrac<11\pi > \right)\) 11) \(\sin \left (x-\dfrac<3\pi > \right)\) Answer \(-\dfrac>\sin x-\dfrac>\cos x\) 12) \(\cos \left (x-\dfrac<5\pi > \right)\) 13) \(\cos \left (x+\dfrac<2\pi > \right)\) Answer \(-\dfrac\cos x-\dfrac<\sqrt>\sin x\) For the exercises 14-19, simplify the given expression. 14) \(\csc \left (\dfrac<\pi >-t \right)\) 15) \(\sec \left (\dfrac<\pi >-\theta \right)\) Answer \(\csc \theta\) 16) \(\cot \left (\dfrac<\pi >-x \right)\) 17) \(\tan \left (\dfrac<\pi >-x \right)\) Answer \(\cot x\) 18) \(\sin(2x)\cos(5x)-\sin(5x)\cos(2x)\) 19) \(\dfrac<\tan \left (\dfracx \right)-\tan \left (\dfracx \right)><1+\tan \left (\dfracx \right)\tan \left (\dfracx \right)>\) Answer \(\tan \left (\dfrac \right)\) For the exercises 20-21, find the requested information. 20) Given that \(\sin a=\dfrac\) and \(\cos b=-\dfrac\) , with \(a\) and \(b\) both in the interval \(\left [ \dfrac<\pi >, \pi \right )\) , find \(\sin (a+b)\) and \(\cos (a-b)\). 21) Given that \(\sin a=\dfrac\) and \(\cos b=\dfrac\), with \(a\) and \(b\) both in the interval \(\left [ 0, \dfrac<\pi > \right )\), find \(\sin (a-b)\) and \(\cos (a+b)\). Answer \(\sin (a-b)=\left ( \dfrac \right )\left ( \dfrac \right )-\left ( \dfrac \right )\left ( \dfrac<2\sqrt> \right )=\dfrac<4-6\sqrt>\) \(\cos (a+b)=\left ( \dfrac \right )\left ( \dfrac \right )-\left ( \dfrac \right )\left ( \dfrac<2\sqrt> \right )=\dfrac<3-8\sqrt>\) For the exercises 22-24, find the exact value of each expression. 22) \(\sin \left ( \cos^\left ( 0 \right )- \cos^\left ( \dfrac \right )\right )\) 23) \(\cos \left ( \cos^\left ( \dfrac> \right )+ \sin^\left ( \dfrac<\sqrt> \right )\right )\) Answer \(\dfrac-\sqrt>\) 24) \(\tan \left ( \sin^\left ( \dfrac \right )- \cos^\left ( \dfrac \right )\right )\)
For the exercises 25-32, simplify the expression, and then graph both expressions as functions to verify the graphs are identical. 25) \(\cos \left ( \dfrac<\pi >-x \right )\) Answer \(\sin x\)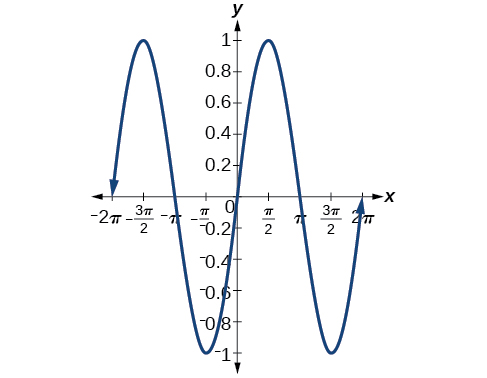 
26) \(\sin (\pi -x)\) 27) \(\tan \left ( \dfrac<\pi >+x \right )\) Answer \(\cot \left ( \dfrac<\pi >-x \right )\) 
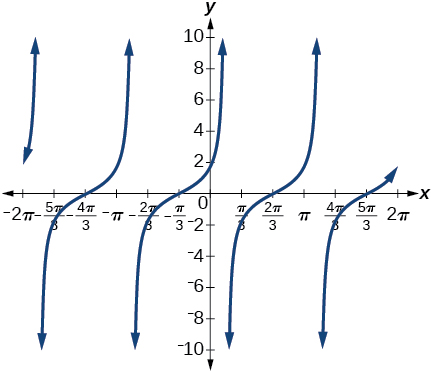28) \(\sin \left ( \dfrac<\pi >+x \right )\) 29) \(\tan \left ( \dfrac<\pi >-x \right )\) Answer \(\cot \left ( \dfrac<\pi >+x \right )\) 
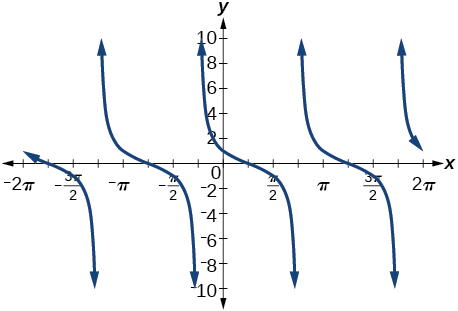30) \(\cos \left ( \dfrac<7\pi >+x \right )\) 31) \(\sin \left ( \dfrac<\pi >+x \right )\) Answer \(\dfrac<\sqrt>+\dfrac<\sqrt>\) 
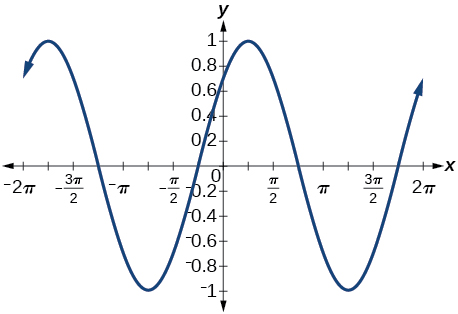32) \(\cos \left ( \dfrac<5\pi >+x \right )\) For the exercises 33-41, use a graph to determine whether the functions are the same or different. If they are the same, show why. If they are different, replace the second function with one that is identical to the first. (Hint: think \(2x=x+x\)) 33) \(f(x)=\sin(4x)-\sin(3x)\cos x, g(x)=\sin x \cos(3x)\) Answer They are the same. 34) \(f(x)=\cos(4x)+\sin x \sin(3x), g(x)=-\cos x \cos(3x)\) 35) \(f(x)=\sin(3x)\cos(6x), g(x)=-\sin(3x)\cos(6x)\) Answer They are different, try \(g(x)=\sin(9x)-\cos(3x)\sin(6x)\) 36) \(f(x)=\sin(4x), g(x)=\sin(5x)\cos x-\cos(5x)\sin x\) 37) \(f(x)=\sin(2x), g(x)=2 \sin x \cos x\) Answer They are the same. 38) \(f(\theta )=\cos(2\theta ), g(\theta )=\cos^2\theta -\sin^2\theta\) 39) \(f(\theta )=\tan(2\theta ), g(\theta )=\dfrac\) Answer They are different, try \(g(\theta )=\dfrac\) 40) \(f(x)=\sin(3x)\sin x, g(x)=\sin^2(2x)\cos^2x-\cos^2(2x)\sin2x\) 41) \(f(x)=\tan(-x), g(x)=\dfrac\) Answer They are different, try \(g(x)=\dfrac\)
For the exercises 42-46, find the exact value algebraically, and then confirm the answer with a calculator to the fourth decimal point. 42) \(\sin (75^)\) 43) \(\sin (195^)\) Answer \(-\dfrac-1>>\), or \(-0.2588\) 44) \(\cos (165^)\) 45) \(\cos (345^)\) Answer \(\dfrac>>\), or \(-0.9659\) 46) \(\tan (-15^)\)
For the exercises 47-51, prove the identities provided. 47) \(\tan \left ( x+\dfrac<\pi > \right )=\dfrac\) Answer \(\begin \tan \left ( x+\dfrac<\pi > \right ) &= \\ \dfrac \right )> \right )> &= \\ \dfrac &= \dfrac \end\) 48) \(\dfrac=\dfrac\) 49) \(\dfrac=1-\tan a \tan b\) Answer \(\begin \dfrac &= \\ \dfrac- \dfrac &= 1-\tan a \tan b \end\) 50) \(\cos(x+y)\cos(x-y)=\cos^2x-\sin^2y\) 51) \(\dfrac=\cos x\dfrac-\sin x \dfrac\) Answer \(\begin \dfrac &= \\ \dfrac &= \\ \dfrac &= \cos x\dfrac-\sin x \dfrac \end\) For the exercises 52-, prove or disprove the statements. 52) \(\tan (u+v)=\dfrac\) 53) \(\tan (u-v)=\dfrac\) Answer True 54) \(\dfrac=\dfrac\) 55) If \(\alpha ,\beta\) , and \(\gamma\) are angles in the same triangle, then prove or disprove \(\sin(α+β)=\sin γ\). Answer True. Note that \(\sin (\alpha +\beta )=\sin (\pi -\gamma )\) and expand the right hand side. 56) If \(\alpha ,\beta\), and \(\gamma\) are angles in the same triangle, then prove or disprove \(\tan \alpha +\tan \beta +\tan \gamma =\tan \alpha \tan \beta \tan \gamma\).
In this section, we will investigate three additional categories of identities. Double-angle identities are derived from the sum formulas of the fundamental trigonometric functions: sine, cosine, and tangent. Reduction formulas are especially useful in calculus, as they allow us to reduce the power of the trigonometric term. Half-angle formulas allow us to find the value of trigonometric functions involving half-angles, whether the original angle is known or not.
1) Explain how to determine the reduction identities from the double-angle identity \(\cos(2x)=\cos^2x-\sin^2x\) Answer Use the Pythagorean identities and isolate the squared term. 2) Explain how to determine the double-angle formula for \(\tan(2x)\) using the double-angle formulas for \(\cos(2x)\) and \(\sin (2x)\). 3) We can determine the half-angle formula for \(\tan \left ( \dfrac
6) If \(\cos x =\dfrac\), and \(x\) is in quadrant \(\mathrm\).
7) If \(\cos x =-\dfrac\), and \(x\) is in quadrant \(\mathrm\).
8) If \(\tan x =-8\), and \(x\) is in quadrant \(\mathrm\).
For the exercises 9-10, find the values of the six trigonometric functions if the conditions provided hold.
9) \(\cos(2\theta )=\dfrac\) and \(90^\leq \theta \leq 180^\)
\(\cos \theta =-\frac>,\sin \theta =\frac<\sqrt>,\tan \theta =-\frac,\csc \theta =\sqrt,\sec \theta =-\frac<\sqrt>,\cot \theta =-2\)
For the exercises 11-12, simplify to one trigonometric expression.
11) \(2\sin \left ( \dfrac<\pi > \right )2\cos \left ( \dfrac<\pi > \right )\)
\(2\sin \left ( \dfrac<\pi > \right )\)
12) \(4\sin \left ( \dfrac<\pi > \right )\cos \left ( \dfrac<\pi > \right )\)
For the exercises 13-19, find the exact value using half-angle formulas.
13) \(\sin \left ( \dfrac<\pi > \right )\)
15) \(\sin \left ( \dfrac<11\pi > \right )\)
16) \(\cos \left ( \dfrac<7\pi > \right )\)
17) \(\tan \left ( \dfrac<5\pi > \right )\)
18) \(\tan \left ( -\dfrac<3\pi > \right )\)
19) \(\tan \left ( -\dfrac<3\pi > \right )\)
For the exercises 20-23, find the exact values of a) \(\sin \left ( \dfrac \right )\) b) \(\cos \left ( \dfrac \right )\) , and c) \(\tan \left ( \dfrac \right )\) without solving for \(x\) , when \(0^\leq \theta \leq 360^\)
20) If \(\tan x =-\dfrac\), and \(x\) is in quadrant \(\mathrm\).
21) If \(\sin x =-\dfrac\), and \(x\) is in quadrant \(\mathrm\).
22) If \(\csc x =7\), and \(x\) is in quadrant \(\mathrm\).
23) If \(\sec x =-4\), and \(x\) is in quadrant \(\mathrm\).
For the exercises 24-27, use Figure below to find the requested half and double angles.
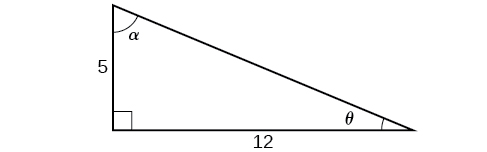
24) Find \(\sin (2\theta )\), \(\cos (2\theta )\) , and \(\tan (2\theta )\).
25) Find \(\sin (2\alpha )\), \(\cos (2\alpha )\), and \(\tan (2\alpha )\).
26) Find \(\sin \left (\dfrac \right )\), \(\cos \left (\dfrac \right )\), and \(\tan \left (\dfrac \right )\).
27) Find \(\sin \left (\dfrac \right )\), \(\cos \left (\dfrac \right )\), and \(\tan \left (\dfrac \right )\).
For the exercises 28-33, simplify each expression. Do not evaluate.
32) \(4\sin (8x)\cos (8x)\)
33) \(6\sin (5x)\cos (5x)\)
For the exercises 34-37, prove the identity given.
34) \((\sin t-\cos t)^2=1-\sin(2t)\)
36) \(\cot x-\tan x=2 \cot(2x)\)
\(\cot (\theta )\tan ^2\theta=\tan \theta\)
For the exercises 38-44, rewrite the expression with an exponent no higher than 1.
